By Aaron Cooper
Assistant Head of School
Summer 2010
My grade 9 students have difficulty appreciating the usefulness of the standard form of the equation of a line, prompting them to ask, ‘When are we ever going to need this?’ This question used to really bother me, and I would look, as a result, for justification for everything I taught. Now I say, ‘Never. You will never use this.’ I then go on to remind them that people don’t lift weights so that they will be prepared should, one day, [someone] knock them over on the street and lay a barbell across their chests. You lift weights so that you can knock over a defensive lineman, or carry your groceries, or lift your grandchildren without being sore the next day. You do math exercises so that you can improve your ability to think logically, so that you can be a better lawyer, doctor, architect, prison warden, or parent. Math is mental weight training. It is a means to an end (for most people), not an end in itself.~Dan Sherman
(from the book “Made to Stick: Why Some Ideas Survive and Others Die” by Dan and Chip Heath)
The Three-Year-Old Program
How Can I Find Out?
On a May morning, a student entered her classroom to find a small group of classmates playing in the sandbox. She counted five children (including herself). She asked her teacher how many students had not yet arrived at school. The teacher asked her if she could think of a way to find the answer to that question. The student thought for a moment before walking to the cubby area. After remembering which students were playing in the sandbox, she began counting the cubbies of the children who were not present. Once she finished, she proudly announced that nine of the children had not yet arrived. The teacher asked her how she came up with that number. The student said she counted the cubbies of the nine missing children. When she added those nine to the five children present, the answer was the magic number, fourteen (the total number of students in the class).
Kindergarten
Would I Be Able To?
Taking polls and making graphs has been a focus for the kindergarten students throughout the year. Students are asked to answer questions by placing a colored cube in the appropriate column in a bar-graphing board. For example, this year students predicted whether certain liquids would freeze in the winter (juice and paint, yes; oil, no) and in another example, identified their preferred Jack-O-Lantern face, scary or happy (scary was preferred by a landslide).
One student in the class was planning a birthday celebration. He wanted to make cupcakes for his class, frosted with each student’s favorite flavor. He brought colored stickers and a list of his classmates to school one morning and set about taking a poll. His teacher asked him how he was going to keep track of the group’s preferences. Remembering his experience with graphing, he decided to use the same method to keep track of his classmates’ frosting choices for his special day. He offered the choices, used the bar-graphing board along with the cubes his class had used all year long, and graphed the results. The student noticed that chocolate was the most popular frosting, and his graph made it possible to see at a glance how many cupcakes of each flavor were required.
Did I Do Something Like This Before?
In second grade, our children develop problem solving skills in geometry by learning to identify and name various shapes. In one activity, the students were given a set of four triangles and four rectangles previously cut from a four-inch square of paper. The students were asked to name the shapes they saw and identify similarities and differences between them.
The class agreed that all the triangles were congruent (in their words, “exactly the same size and shape”) and noticed that all the rectangles were congruent as well. Then, the students were given a pair of scissors and a new, unmarked four-inch square piece of paper and asked to cut four congruent triangles and four congruent rectangles from it with no leftover paper (fig.1). Teachers noted that there was plenty of extra paper, if needed.
Some students got to work folding and cutting by trial and error. Others tried to envision the problem before beginning to cut. One student tried to start cutting out shapes approximately the correct size. After getting two triangles and two rectangles, none exactly the same, she was left with scraps of paper littering her desk. A teacher approached her, and they started a discussion. The teacher asked if she remembered the quilting squares project they completed a couple of week before. The student did. “Now, what shapes were on that quilt? How did you make those shapes?” The student remembered that there were rectangles and triangles and that she had folded the paper first before making her quilting design. Off she went, folding and cutting. Five minutes later, she proclaimed happily, “I got it!” and showed off her eight shapes with no leftovers.
Grade Four
Is There A Pattern?
On a beautiful June morning, fourth grade students gathered in the Grace Muller Courtyard to work on a problem about King Arthur selecting a knight to marry his daughter. At first, there were thirty knights around the table. King Arthur eliminated every other knight, starting with the second knight and continuing around the table until there was only one knight left. What was the seat number of the lucky knight?
Students scattered in pairs around the courtyard, armed with sidewalk chalk and a copy of the question. They drew circles, made slashes, used multiple colors and checked their work using different methods. When they gathered together five minutes later, most had determined that seat #29 was the lucky seat.
The second part of the problem asked students to figure out a winning strategy for a more complex game. If I were a knight wishing to be chosen to marry the king’s daughter, and I did not know in advance how many knights would be at the table, is it possible for me to figure out where is the best place to sit? Can I show up the day of the competition, count the knights, think for a minute, and then take a seat that I know will make me the winner?
Before the students got to work, the teacher asked what strategies they might use to solve problems like this. Students called out possibilities. “Draw it!” said one. “Try to find a formula!” and “Use a calculator!” said others. The teacher asked if the students remembered how they had solved a recent problem called, “The Ice Cream Problem.” A student said, “We tried to find a pattern; maybe that will work here.” The teacher agreed.
When the students scattered to begin searching for the pattern, they agreed on a systematic approach to solving the problem: start with one knight at the table, continue adding a knight and tracking the “magic” seat until a pattern emerges.
It is quite a complex pattern but the students were able to get at it bit by bit. First, they noticed that the first knight wins again and again. Then, the students noticed that an ever-increasing sequence of consecutive odd integers gave the place of the winning knight. As can be seen in fig. 2, the odd integers, starting with one, repeat themselves to give the place of the winning knight. Each time, the string of odd integers lengthens. Eventually the students noticed that the first knight wins when there are two knights, four knights, eight knights….. and on and on as the number of knights doubles, beginning with two.
After much discussion, they learned to predict the correct seat for a given number of knights. While not explicitly writing a formula, the students realized that they needed to find the highest power of two that was a part of the number of knights at the table. The number left over from that power of two was the winning position! Explicitly formulating the problem would require the use of logarithmic functions, a high school math topic often learned in pre-calculus courses.
Nevertheless, our fourth graders were able to appreciate the pattern and use it to model the problem. This kind of thinking lays the groundwork for a much deeper understanding of such problems when encountered in more advanced classes, where the actual formula will be the end product of the exercise.
Grade Six
There Must Be An Easier Way
A sixth grade class starting their study of permutations and combinations had completed the following problem for homework: “The digits 1,2,3, and 4 are written on slips of paper and placed in a hat. A three-digit number is drawn at random from the hat. What is the probability that the three-digit number is divisible by the number three?”
Students presented their methods for solving the problem: “I wrote out all the possibilities of a three-digit number – there are 24,” and “I did 4! (four factorial - i.e., 4x3x2x1) to determine 24 possibilities.” Another student noted that each number sequence (such as {1,2,3}) had six possible combinations and that no matter the order, each of those numbers will be divisible by three. {2,3,4} was another set of numbers divisible by 3 with six combinations. So, the class agreed that the answer was ½: 12 out of the possible 24 combinations would be divisible by three.
During the ensuing conversation about how students checked their answers, a hand shot up from the side of the classroom. “What if there were 1,000 numbers in the hat instead of four?” Mathematicians love this type of question. They call it the “natural” next step, a more difficult question of the same type. The teacher, knowing that this is what mathematicians do, engaged the question. “Okay,” she said, “Let’s change it. Instead of four digits in the hat, there are ten. Zero through nine. The other parameters are the same. Get to work.”
The students began by using the tried-and-true method from the original problem, writing out all the possible number sequences that are divisible by three. As students called out numbers and the teacher wrote them on the board, some students began to wonder if they’d chosen the best method. They asked, “How can we be sure that these are the only possibilities?” and “Is there a better way to do this?” “All this work, and we’ve probably got it wrong,” said some. Though the students made good progress on the problem, they soon discovered that their original methods were unreasonably time consuming and difficult for this extended problem. In the end, they were close. The students found forty sequences divisible by three, yielding 218 combinations. There are, actually, forty-two sequences yielding 228 combinations and a probability of 19/54 (approximately 35%) of getting a number divisible by three.
When mathematicians encounter a similar issue – known methods being overly cumbersome, they have two options: automate the original method, if possible, or develop a stronger method. The students’ recognition that there must be a simpler way to solve the problem and subsequent attempts to identify that method is an important step in the development of their mathematical minds.
The solution requires a more advanced form of combinatorics, usually studied in high school pre-calculus classes. The students saw how the more advanced problem is motivated from the simpler problem. Further, they began to explore the more advanced problem and develop techniques for solving it. Both of these experiences should deepen their understanding of the topic when they come to study it in a more formal fashion in high school.
Grade Eight
It’ll Be Some Crazy Shape…Or, Maybe, A Parabola
Towards the end of the school year, an eighth grade math class began with the following pep talk: “You all know a lot at this point in the year. Now, can you work on a problem that could use any of the things you’ve learned? Even if I don’t tell you which of those things you’ll need to use? Trust me, you know how to do this. It may look strange and feel strange, but you’ll figure it out. You know how.”
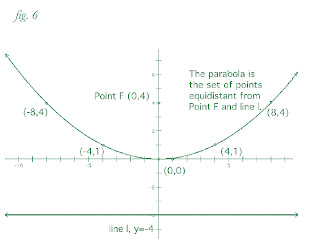
The teacher then asked students to remind one another about two concepts that they had derived the previous day: how one finds the distance between two points on a graph (fig. 3) and how to determine the shortest distance between a point and a line (fig. 4). Afterwards, the teacher continued, “Good. Now, suppose I have a point, F, at (0,4) and a horizontal line, l, with the equation y=-4. Find a point or some points that are equidistant from F and l.” A student’s hand shoots up. “I got one! (0,0) is four units away from both the line and the point.” The teacher responded, “Excellent. Now, can someone get another?” 
After a number of guesses – many close but none correct – students began thinking of the shape that might appear. “It’ll be some sort of crazy shape...or, maybe, a parabola.” “Yeah, maybe the origin, (0,0), is on the axis of symmetry,” and “You could reflect the other points.” The teacher re-centered them, “Okay, but so far you’re guessing. Let’s find another point that we are sure about and go from there.”
Another minute passed. A different hand shot up. “I got one! (4,1) is five units above the line and, if you use the distance formula, you find that it is also five units away from the point F.” “Very good.,” said the teacher. Another student offered, “And its reflection, (-4,1), also works!” Soon, another student had found two more points, (8,4) and (-8,4), that were also equidistant from F and l. The teacher, cycling back to the students’ previous hypotheses, said, “Excellent.
So, we have a lot of questions. Is this a parabola? Is it a parabola segment? Is it some sort of ‘V’ shape? What is it? There are a variety of conjectures, but the strongest consensus is behind the idea that all the points together will form a parabola. So, how do we confirm this conjecture? This is the next step. Let’s take a sliding point, (x,y), that satisfies the given requirements, but that could be anywhere on the resulting shape. Find out how far the point, (x,y), is from F and how far it is from l.”
The students got to work. After ten minutes of conversation, of building on one another’s ideas, of trying some thoughts that proved incorrect and others that proved helpful, the students were able to determine the distances that (x,y) is from F and l.
They then realized that to get the equation describing the resulting shape, they would need to set the two expressions equal. The students had taken a similar approach when deriving the equation for a straight line earlier in the year. Although this problem was significantly more difficult, they were able to come to that realization with only very little reminder.
The next day, they completed the problem (fig. 5) and discovered that they had indeed derived the equation of a parabola (fig. 6).